Answer to Question #9367 Submitted to "Ask the Experts"
Category: Instrumentation and Measurements — Instrument Calibration (IC)
The following question was answered by an expert in the appropriate field:
I am developing an instrument which measures the volumetric activity of beta particles (i.e., 85Kr) in air. I am using an end-window Geiger Muller (GM) counter. The air will be pumped via a filter through a one-liter enclosed chamber. We have kept the flow rate nearly 333 cm3 s-1. Please suggest how I can calibrate this instrument. What is a standard practice for calibration?
The actual air sample is not available for calibration. Can either the disc type or planar type 90Sr+90Yr source be used for calibration, or is there any other theoretical method we may adopt to calculate the volumetric activity in Bq m-3?
The best method to use for calibrating closed or flow-through chamber systems for monitoring beta-emitting airborne radionuclides is to simulate, as well as possible the actual measurement situation using calibrated quantities of appropriate radionuclides. For example, if you are interested in measuring 85Kr, a calibrated quantity of this gas can be injected into a closed loop that contains the one liter chamber and detector assembly, connected through tubing to a small pump that will ensure uniform mixing of the gas in the chamber volume. The exhaust from the pump would be directed through the tubing to the inlet of the chamber, and the exhaust from the chamber would go to the inlet of the pump. It is desirable to keep the void volume of the peripheral tubing and pump as small as reasonable. In addition to the void volume of the chamber, the volume of the tubing and any pump void volume must be known so that the concentration of the 85Kr may be calculated. If you are planning on measuring airborne nuclides that emit different beta energies you should attempt to perform the calibration with nuclides that cover an energy range that includes the range of interest. If the beta radiations from the radionuclides to be measured are very different in energy, the detector response may be significantly different for those radionuclides. This is a problem if you will be attempting to measure mixtures of such radionuclides, since, without other independent assessments of relative amounts, you will not know how much of the detector output is associated with a given radionuclide.
Based on what you have stated, you may not be able to perform calibrations using airborne radionuclides as described above. It is possible to do some mathematical modeling that might allow approximations to the expected detection efficiencies or response factors for the chamber system. Unfortunately, some such modeling may not account accurately for certain factors that might affect results. These include such things as uncertainties in the thickness of the end-window GM detector, effects of backscatter within the chamber, and effects of non-beta radiations that might be emitted by the radionuclides of interest. The most powerful modeling technique is probably Monte Carlo simulation. If you have not used Monte Carlo procedures, the learning curve is rather steep, and some monetary investment is necessary to purchase a suitable computer code if one is not available to you. One of the most popular of the Monte Carlo codes is the MCNP-5 code available from the Oak Ridge Radiation Safety Information Computational Center.
You inquired about the possibility of using disc/planar sources of 90Sr-90Y in an experimental measurement process to attempt to determine an appropriate calibration factor for the volume detection system. Such a process is possible but is naturally subject to possible errors associated with approximation techniques and simplifying assumptions used in the analysis. Because the response of the detector may be greatly influenced by the energies of the beta particles, you must attempt to use beta emitters that are representative if the energies of interest. The 90Sr as a calibration radionuclide is not a good choice to simulate 85Kr (maximum energy about 0.67 MeV) because the 90Sr (maximum energy about 0.55 MeV) will always contain the high-energy beta emitting daughter radionuclide 90Y (maximum energy about 2.28 MeV).
I shall attempt to demonstrate the geometry considerations involved in some approximation methods, first assuming we have a uniform planar source of the same cross sectional area as the proposed chamber volume. There are also mathematical approximation methods that may be used in which a small area or point source may be used to obtain an estimation of the volume source calibration factor, and we shall also briefly consider these, but for now let us assume the planar source. The assumed geometry is as shown below.
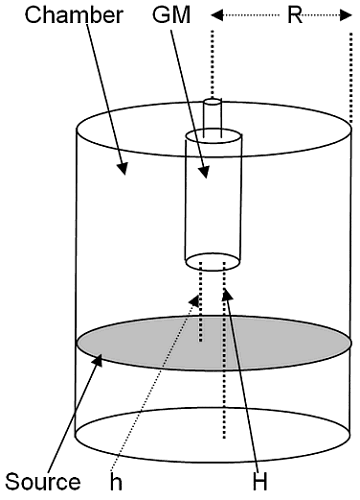
You do not specify the shape of the chamber volume or the orientation of the detector. In the above sketch I have assumed that the detector is at least partly inserted into the chamber volume, that the volume of the chamber is cylindrical in shape, and that the GM detector is a typical end-window type. We shall assume that airborne radioactivity located beyond the detector window plane (greater than height H) does not contribute to the detector response. This may not be true if the detector wall thickness is less than the ranges of the beta radiation of interest. Additionally, some beta radiation emitted from beyond H may be scattered back from the inner chamber wall into the detector window. Naturally, if the detector was mounted so that the detector window was flush with the inner chamber flat wall face and facing into the chamber volume, the concerns with scatter of beta radiation from airborne activity would not prevail. The use of a disc source may result in backscatter of source beta particles from the source support that may also produce some response.
If we imagine that the distance H is subdivided by imaginary planes, parallel to the chamber flat faces, into n equal acceptably small thickness intervals, each ΔH, we can specify the volume of each squat cylinder formed by two sequential planes and the chamber walls as πR2ΔH. If we measure the detector net count rate when the planar disc source, with activity per unit area equal to SA, is at distance h from the detector window, and h is selected to fall midway between two imaginary planes separated by ΔH, and we specify this count rate as Ci, we can write a simple expression that represents the expected count rate per unit activity concentration, Cexp—e.g., cpm/Bq-cm-3.
| n | ||
| Cexp = | (ΣCi) | /(SA/ΔH) (1). |
| i=1 |
In general, the smaller the ΔH separation between imaginary planes, the greater will be the accuracy of the estimate.
Below is an example set of hypothetical data that is intended to represent experimental count rates obtained when a planar disc source with a radius of about 5 cm and an activity area concentration of 145 Bq cm-2 of a pure beta emitter is placed at different distances h from the detector window. The chamber volume is assumed to be cylindrical with an inner radius of 5 cm; the detector is assumed to project a short distance (2–3 cm) into the chamber, and H = 10 cm.
| Distance, h (cm) | Net Count rate, cps |
|---|---|
| 0.5 | 167 |
| 1.5 | 90.4 |
| 2.5 | 58.4 |
| 3.5 | 40.3 |
| 4.5 | 29.2 |
| 5.5 | 21.8 |
| 6.5 | 16.8 |
| 7.5 | 13.3 |
| 8.5 | 10.8 |
| 9.5 | 8.87 |
Summing the count rates we obtain:
| 10 |
| ΣCi = 457 cps. |
| i=1 |
Neglecting any dead time losses and applying equation 1, we obtain:
If instead of 1 cm depth increments we had selected 2 cm increments and used only the count rates at 1.5 cm, 3.5 cm, 5.5 cm, 7.5 cm, and 9.5 cm we would have obtained 2.41 cps/Bq-cm-2, a result significantly less than that obtained using the thinner depth increments.
If the planar source of required dimensions was not available, an alternative estimation could be made using a point source or an area source whose dimensions were significantly smaller than the window area of the detector. In such an instance we could imagine that the cross-sectional area of the chamber was divided into a number of annular rings, here taken as all of the same area. If desired, the area at the center could be a complete circular disc rather than a ring, but its area should be the same as the area of each annular ring for this example. The sketch below shows a plan view (not to scale) of the division of the cross-sectional area of the chamber into rings of equal areas. Naturally, the widths of rings of greater radii are less than those of smaller radii.

A count rate, Ci, is obtained when the small source of strength S (e.g., Bq) is approximately centered along the width of each annular area along the respective radius (i.e., if ri and ri+1 are the radii that define the annulus, the source would be centered at about (ri+ri+1)/2). The count rate, Cd, to be ascribed to the complete disc area, lying distance h (first sketch above) from the detector window, and represented by the sum of all m of the annular (and central) areas would be simply
| m | |
| Cd = | ΣCi (2). |
| i=1 |
If we then imagine the set of annular rings (plus central area) to be moved by the small vertical increment ΔH, and we then repeat a similar counting operation for the source and each annular ring and do the same for all n depth increments (separated one from the next by depth interval ΔH) along H (first drawing above) we can write the expected total count rate per unit activity volume concentration, Ctot, as
| n | |
| Ctot = ( | ΣCd)/(S/ΔAΔH) (3). |
| d=1 |
where ΔA represents the area of one of the annular rings i.e., π(ri+1 – ri)2. Here again, the smaller the areas of the annular rings and the smaller the depth increments, the greater will be the expected accuracy.
This analysis could also be performed for annular rings that are not of equal area (e.g., annular rings of equal width) in which case, if the source of activity S were placed at the mid-width of each ring, the activity per unit volume to be used in the approximation would be given by S/ΔAiΔH; the incremental area of the ith ring annular ring element would be given by π(ri+1–ri)2. Since the area elements would not be equal, the count rate per unit activity volume concentration would have to be assessed for each element to obtain the final response factor—e.g., at the selected distance h from the window, the expected count rate per unit activity volume concentration would be
| m | |
| Cv = | ΣCi/S/ΔAΔH (4). |
| i=1 |
The expected total count rate per unit activity volume concentration, accounting for contributions from all depth increments along H would then be
| n |
| Ctot = ΣCv (5). |
| d=1 |
As noted earlier, these types of analyses improve in accuracy as incremental sizes are reduced. This is especially true when the source elements are close to the detector. You must pay attention to the energies of the beta radiations involved to ensure that your calibration is legitimate for the radionuclides of interest. You must also consider possible influences of other radiations (e.g., gamma rays, x rays, conversion electrons) from either the field radionuclides of concern or from the calibration radionuclides that could affect the actual count rates. Additionally, if the yields of the beta rays of interest are different for the calibration radionuclide(s) and the field radionuclide(s) you must adjust your calibration results to account for this.
While I am not familiar with any published formalized methodologies for using point or area sources to simulate results from volume sources, as in this case, there are some cases where such methods have been applied. One example in which a point source is used to calibrate (determine counting efficiency of) an end window GM detector for use in measuring area sources is given in NCRP Report No. 112, Calibration of Survey Instruments used in Radiation Protection for the Assessment of Ionizing Radiation Fields and Radioactive Surface Contamination, Dec. 1991 (pages 109–110).
I hope this is helpful to you.
George Chabot, PhD, CHP


