Answer to Question #8629 Submitted to "Ask the Experts"
Category: Instrumentation and Measurements — Instrument Calibration (IC)
The following question was answered by an expert in the appropriate field:
I have seen a paper about GAFCHROMIC films (Butson et.al, Applied Radiation and Isotopes (64):60-62; 2006) that gives the measured values of the energy dependence (relative response as compared to 60Co) from 28 keV and above. No measurements have been done below this energy (at least I am not aware). I am interested in measuring the doses resulting from synchrotron radiation by using the same GAFCHROMIC EBT film as used by Professor Butson. The synchrotron (x-ray) energy is likely to vary from 1 keV to 40 keV. The GAFCHROMIC EBT film is reported to be nearly energy independent above 28 keV. However, at low energies its relative response (energy dependence) is not known. How can I determine the dose accurately? Has anyone measured the relative response below 28 keV? Can the response factors be determined theoretically?
I also am not aware of any photon-energy-dependent studies that have been done for the GAFCHROMIC EBT films below the 28 keV energy to which you refer. The film was developed particularly for applications in medical therapy, especially for work involving intensity modulated radiation therapy, and, as such, the major interests are in higher-energy photons.
There are some possible approaches to attempt to establish the energy-dependent dose response of the film in the energy range of interest to you—i.e., from 1 keV to 40 keV. Probably the most effective manner to make such estimations is to run Monte Carlo simulations for the energies (and geometries) of interest. If this approach is not available to you, there are some other possible deterministic approaches that may be helpful.
At the very low-energy end of the distribution of interest to you, the interactions are dominated by the photoelectric effect. According to specifications that I have found for the film in a white paper from International Specialty Products (ISP), the active region consists of two 17-micron-thick layers separated by a 6-micron-thick layer, and both outer large surfaces of the film are covered by a protective layer of polyester film, each such layer being 70 microns in thickness.
Assuming that this covering material is similar to a commonly used polyester such as polyethylene terephthalate (Dupont mylar), the 70-micron layer would be sufficient to stop pretty much all 1 kev photons incident on it. Two keV photons would penetrate to the extent of about 2%. At 3 keV the penetration would be close to 30%, at 5 keV around 75%, and about 97% at 10 keV. For estimation purposes, it is reasonable to assume that most all of the interactions that occur in the active film at these low energies will be by the photoelectric effect. Then, for a beam of photons incident normally on the film surface, the average dose delivered throughout the active region, Davg, may be related to the dose at the protective outer surface by, Ds, by
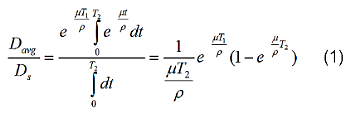
where µ/r is the mass attenuation coefficient for the film material (here it is assumed that the mass attenuation coefficient for the protective layer and the active medium are the same), T1 is the mass density thickness of the protective layer, and T2 is the total mass density thickness of the active material (note that in the calculations done here I have added the 6-micron-thick layer to the two 17-micron-thick active regions in evaluating the average dose through the active material).
Assuming the entire composition is the same as that of mylar, I have done some simple calculations to evaluate equation 1 at energies from 1 keV to 30 keV. Note that in these calculations I have assumed a standard density of 1.4 g cm-3 for the material (this is the usual density of mylar). Above about 5 keV, although the photoelectric effect is still dominant up to perhaps 20 keV, the Compton scatter cross section is increasing and dose may be influenced by the scattered photons at the higher energies, and these are not considered in the calculations. I have attached a spread sheet showing the input data and results, and the table below summarizes the results of evaluating equation 1, as well as the fractional transmission through the protective layer. The mass attenuation coefficients have been taken from Hubbell (Photon Mass Attenuation and Mass Energy Absorption Coefficients from 1 keV to 20 MeV; Int. J. Appl Radiat Isot (33):1269–1290; 1982).
| Energy, keV | µ/r, cm2 g-1 | e-µT1/r | Equation 1 value, Davg/Ds |
|---|---|---|---|
| 1 | 2,920 | 3.73E-13 | 2.28E-14 |
| 2 | 414.2 | 0.0173 | 0.00671 |
| 3 | 126.2 | 0.290 | 0.208 |
| 4 | 53.42 | 0.592 | 0.512 |
| 5 | 27.26 | 0.766 | 0.710 |
| 6 | 15.68 | 0.858 | 0.821 |
| 8 | 6.58 | 0.938 | 0.920 |
| 10 | 3.395 | 0.967 | 0.958 |
| 15 | 1.106 | 0.989 | 0.986 |
| 20 | 0.570 | 0.994 | 0.993 |
| 30 | 0.298 | 0.997 | 0.996 |
It appears that the film will probably not be useful for photons below about 2 keV. For higher energies, if the atomic composition of the active film region were the same as that of soft tissue (or water if that is the dose material of interest) then the table value at a low energy might be used to get the actual surface dose—e.g., if the film had been calibrated at high photon energies and was then irradiated at normal incidence with 5 keV photons, the surface tissue dose at the film location would be the interpreted dose on the film divided by 0.71. In actuality, the effective atomic number of the active film material is not exactly the same as that of water (or soft tissue). For water the effective atomic number is about 7.3 and that quoted in the above cited ISP paper is 6.98. The photoelectric varies as about the fourth power of the atomic number at low photon energies; thus, the above interpreted surface dose at 5 keV might be approximately (6.98/7.3)4 = 0.84 of the actual water dose.
Another possible approach for assessing the film response at low energies would require using an independent measuring system to measure dose or a related quantity. For example, a thin-window air-ionization chamber could be used to measure dose to air, and this could be converted to water dose by multiplying by the ratio of water to air mass energy-absorption coefficients. Alternatively, if you have access to a suitable thin-window fluence detector, and you can specify the energy of the incident photons, you can calculate dose from the product of the fluence, photon energy, and water mass energy-absorption coefficient.
If you intend to use or perform any calculations as have been done above or any other analyses, you should contact the manufacturer of the film in order to obtain the best information you can about the composition of the film. For instance, the assumption I made about the composition being similar to mylar may not be correct, especially for the active regions. The ISP paper gives the presumed atomic composition, which I assume is for the active material, but the mass density is not provided.
Measurements at the low energies of interest to you are not easy; I wish you well in your endeavors.
George Chabot, PhD, CHP


