Answer to Question #7500 Submitted to "Ask the Experts"

Category: Instrumentation and Measurements — Surveys and Measurements (SM)

The following question was answered by an expert in the appropriate field:

Q

I have a nuclear medicine technician who was contaminated with 99mTc on the finger. The contaminated area was approximately 1 cm2. Initial counts were 1.667 × 101 cps with a DT 304 frisker. How can I calculate the radioactivity involved so I can calculate skin dose?

A

I have not used the military-designated DT-304 detector, but I find that it is a pancake-type Geiger Mueller detector. The response of such a detector will depend, in part, on the type of source used to calibrate it—i.e., radiation type(s) and energies—and on the source/detector geometry. If the detector had been used with a ratemeter and calibrated to read exposure rate from a 137Cs source (137mBa 662 keV photons), the usual arrangement would have been to have the source far enough away from the detector so that the gamma field would have been uniform over the area of the detector window.

If the detector responds similarly to other standard-type pancake probes (which have a window thickness of about 2 mg cm-2 and area of about 15 cm2), I would expect the count rate per unit exposure rate from the 140 keV photons from 99mTc to be about the same as that for the 137Cs. It is likely, however, that for a measurement of skin contamination, as you describe, the detector would have been held very close to the contaminated area, likely more-or-less centered over the activity. Since the contamination area of about 1 cm2 is considerably less than the window area, the window will not be uniformly irradiated. To complicate things somewhat more, during the decay of 99mTc, there are a number of conversion electrons emitted, those of importance lying in the energy range from about 120 to 140 keV. These have a combined yield of about 0.10 electrons per disintegration and are sufficiently energetic to produce a response on the thin-window detector held in proximity to the contamination source.

Given these considerations, the best way of estimating the efficiency for the probe would be to make some direct measurements using a 99mTc source of known activity and in a geometry similar to that used for the actual contamination measurement. Such a source could be prepared by transferring a small volume (preferably no more than about 0.1 ml) to a low-atomic-number surface (something like Lucite would probably be acceptable), allowing the deposit to evaporate and carefully making the measurement(s), taking care not to spread the unsealed activity by contact with the source. The transferred solution would probably come from a previously calibrated 99mTc preparation; it may be necessary to allow the transferred activity to decay if the activity is too high for measurement under the desired conditions (a source strength of less than 3.7 × 104 Bq would probably be adequate).

We can do at least a crude estimate of the expected response of the detector based on consideration of the 140 keV photons alone under the assumption that the detector was calibrated in exposure rate units using a 137Cs source. It is a fairly easy matter to show that for the 137Cs energy, the fluence rate of photons necessary to yield an exposure rate of 7.17 x 10-11 C kg-1 s-1 is about 780 cm-2 s-1. If we consider an arbitrary one 3.7 × 104 Bq 99mTc source whose dimensions are considerably less than the diameter of the detector window, we can evaluate the average photon fluence rate over the window area. This is done through a calculation as below:

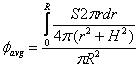     (1)

where it is assumed that the small source of photon emission rate, S, is centered at a distance H below the window whose radius is R and where r represents the variable radius from the center of the window to any point on the window. The solution to this equation is

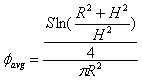      (2).

If we assume a nominal 99mTc activity of 3.7 × 104 Bq, the 140 keV photon emission rate, S, would be 3.296 x 104 s-1. If we further assume that the dimensions of the detector window and its response characteristics are the same as a typical thin-window GM detector with an active area of about 15 cm2 (such as the Model 44-9 manufactured by Ludlum Instrument Co.), we can assign R = 2.185 cm. If we assume a distance H of 0.1 cm from the source and apply equation 2, we would then calculate a value for the average fluence rate over the detector window area of 3.39 x 103 cm-2 s-1. The typical pancake probe yields about 7.67 x 1011 cps per C kg-1 s-1; using this in conjunction with the above-noted fluence rate-to-exposure conversion factor of 7.17 x 10-11 C kg-1 s-1 per 780 cm-2 s-1, we would obtain an expected count rate, C, of

C = (3.39 x 103 cm-2 s-1)(7.17 x 10-11 C kg-1 s-1/780 cm-2 s-1)(7.67 x 1011 cps/C kg-1 s-1) = 2.39 x 102 cps.

Then for an observed count rate of 1.667 × 101 the related source activity would be about 1.667 x 101 cps/2.39 x 102 cps/3.7 x 104 Bq = 2.58 x 103 Bq. We should bear in mind that this calculation accounts only for the contribution to detector response associated with the 140 keV photons. The conversion electrons noted earlier will also contribute to the observed count rate; hence, the actual activity would be lower than this 2.58 × 103 Bq. I would estimate that the electron contribution to count rate would lower the above-calculated activity by at least a factor of two, implying that the activity associated with the 1.667 × 101 cps may be around 1.1 × 104 Bq.

Naturally the above is demonstrative only for the assumed conditions. If the distance of the detector window from the contamination had been 1 cm instead of 0.1 cm, for example, the calculated average photon fluence rate would have been about 3.5 times lower than that calculated above, and the estimated activity would have been 3.5 times higher, or about 9 × 103 Bq. Again, this estimate does not include the effect of the conversion electrons.

In summary, the best approach is to obtain an experimental estimate of the counting efficiency for the conditions consistent with the field measurement that was made. Lacking this, calculations such as the above can provide estimates of activity that can be used in estimating skin dose. The integral dose that might have been delivered to live skin cells depends on the activity as well as other factors, including the half-life of the radionuclide, the residence time on the skin surface, and the thickness of the dead skin layer. I don't know what method of calculation you intend to use for the dose calculation, but I expect that the dose result you calculate will be a very small fraction of the dose limit for the skin. Good luck in your continuing evaluation.

George Chabot, PhD, CHP 

Ask the Experts is posting answers using only SI (the International System of Units) in accordance with international practice. To convert these to traditional units we have prepared a conversion table. You can also view a diagram to help put the radiation information presented in this question and answer in perspective. Explanations of radiation terms can be found here.
Answer posted on 27 May 2008. The information posted on this web page is intended as general reference information only. Specific facts and circumstances may affect the applicability of concepts, materials, and information described herein. The information provided is not a substitute for professional advice and should not be relied upon in the absence of such professional advice. To the best of our knowledge, answers are correct at the time they are posted. Be advised that over time, requirements could change, new data could be made available, and Internet links could change, affecting the correctness of the answers. Answers are the professional opinions of the expert responding to each question; they do not necessarily represent the position of the Health Physics Society.