Answer to Question #10000 Submitted to "Ask the Experts"
Category: Instrumentation and Measurements — Surveys and Measurements (SM)
The following question was answered by an expert in the appropriate field:
I am examining the detection limits in a case where my background is spatially varying and I am examining how to use that data set in determining detection limits. For example, I measure the radiation level in 100 different locations, where the background changes from location to location (100 different houses constructed of various materials). I now want to determine the detection limit for future studies of additional locations in the same general area. I have reviewed the statistics equation and thought about just using the measured standard deviation as the standard deviation of background (the square root of the average background count) instead of making the normal approximation. But that just seems too easy. What is the correct path? Also, is there a good reference for counting statistics when the background is varying by location and/or time in addition to the normal random probability fluctuations?
Dealing with a population of measurements that shows appreciable variability can lead to difficulties in decision making and reaching conclusions in which you have a reasonable level of confidence. If there are means of legitimately reducing the variability, such approaches can be productive. You say that you are measuring radiation levels, but you do not specify how the measurements are being made—for example, are they external radiation dose rates? If so, are they being measured with an analog ratemeter or are you using a digital survey instrument? This can influence how you evaluate the standard deviation associated with each reading. If you are accumulating counts over a fixed time interval, then the standard deviation in the count is, as you have noted, the square root of the count, but this would not apply if you were using an analog ratemeter (see Question 8067 and its answer on the Health Physics Society "Ask the Experts" website; you might also want to look at Question 8910). I would generally recommend using the experimental standard deviation to reflect the variability beyond the counting statistics.
You cite the instance of measuring radiation levels in 100 different houses as an example. If you have observed variations in levels that are associated with differences in building materials, such causes of variability constitute nonrandom sources; they represent systematic sources of variation in measured readings. In such cases, you might be able to group the houses according to building materials, building design, or the like to define more than one population of test subjects, each population being subject to normal statistics. In these instances, each population (for example, wood-frame houses, brick houses, natural-stone houses) would be associated with its own normal statistics, such as a mean radiation level and an associated standard deviation. The experimental sample variance, which is the square of the standard deviation, may be calculated in the usual fashion from your respective set of N measurements, the ith measurement being defined as xi and the mean of the measurements being x:
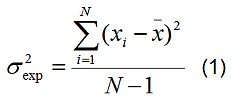
If you believe that differences in construction materials are producing differences in measured radiation levels, you can perform statistical tests to evaluate whether the respective mean values of two subpopulations are in fact statistically different. If there are other influencing factors, such as notable changes in elevation, differences in geology, or time dependencies associated with measurable differences in radiation levels, these could also be considered in grouping of your measurement results. Minimizing the influences of systematic influences in this fashion may reduce the uncertainties associated with your measurements and provide for more powerful testing of real changes that might exist among measurements.
If you have separated data into two groups, A and B, that you determine or hypothesize have different mean radiation levels, you can check for the statistical significance of this difference by performing an appropriate test. One of the most useful and common such tests for comparing the means of two sets of data is the Student's t-test. The t-test applies if the distributions of data that you are comparing are normal or near normal. The t-test works by generating the t-statistic that represents the ratio of the difference between the two means divided by the estimate of the standard deviation of the distribution of sample mean differences:
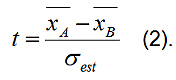
The value of t is then compared against published table values for a specified number of degrees of freedom (the number of degrees of freedom would normally be NA – 1 + NB – 1 where NA and NB are the respective number of measurements in groups A and B) to evaluate the probability that such a value could arise out of random variations. The null hypothesis normally tested is that the two means are not statistically different. If the t-test yields a value that is a sufficiently small probability, we would conclude that the two means are likely different. You can find this test discussed in most statistics textbooks. A convenient online text of common statistical methods and concepts, Concepts and Applications of Inferential Statistics, is available through Vassar College. Click on Table of Contents and refer to Chapter 11 to read about the t-test.
If you find that the subpopulations you have defined are not statistically distinct, or if you are otherwise unable to separate your population of measurement locations into more tightly grouped subpopulations, even though you recognize that there are influencing factors that are producing systematic uncertainties, then you will have to deal with the possibly greater uncertainties that accrue because of the greater variability inherent in the entire population. In such an instance, systematic errors/uncertainties are often treated as though they were random. If the distribution of measurements is reasonably normal, you can calculate the experimental standard deviation associated with the measurements, using normal statistics.
If the distributions you are dealing with are clearly not normally distributed, there may be other, less common options for making judgments regarding their variability and whether or not two populations are significantly different. One common observation in a lot of environmental data is that the data are often skewed to the right (long tail at higher values). Such data can often be handled by treating the distribution as a log-normal distribution in which the log-normal variable y is related to the normal variable x by the relationship y = ex. When log-normal data are plotted on log-normal (base 10) probability paper so that the base 10 logarithm of the variable is plotted against the cumulative percentage of observations with magnitude less than y, one should obtain a near straight line. The defining parameters are the geometric mean and geometric standard deviation. The geometric mean of the data is the value at the 50% cumulative frequency. The geometric standard deviation is given by the ratio of the y-value at the 84% cumulative frequency divided by the y-value at the 50% frequency (the geometric standard deviation can also be obtained by the y-value ratio at 50% frequency to that at 16% frequency).
For comparisons between sets of data that do not meet normal or log-normal criteria, other tests that do not rely on any assumptions about distribution shapes may be used. The Mann-Whitney test is one such test in which data are ranked from 1 to N in terms of increasing values of the data points, but with no other regard to the specific values. The rank values and numbers of data points are then manipulated to generate statistical results that are used to make judgments about the distinctions between distributions. If you have an interest in this and other tests that do not rely on standard techniques that we apply to common distributions, you can find some descriptions and examples in the previously cited Vassar online document (Chapter 11a shows how the Mann-Whitney test works).
There are many textbooks and online sources available that deal with statistics. Many are not specific to radiation measurements, but the basic concepts discussed are often applicable. A couple of statistics texts that I have found useful are Data Reduction and Error Analysis for the Physical Sciences (Philip R. Bevington and D. Keith Robinson, McGraw-Hill Book Company, 1992) and Mathematical Statistics with Applications (Dennis D. Wackerly, William Mendenhall, and Richard L. Scheaffer, Duxbury Press, 1996). There are also useful discussions of commonly applied statistics in some of the more popular radiation science and protection textbooks, for example, Introduction to Health Physics: Fourth Edition (Herman Cember and Thomas E. Johnson, McGraw Hill, 2009) and Radiation Detection and Measurement, Fourth Edition (Glenn F. Knoll, Wiley, 2011). If you are a member of the Health Physics Society, you can also find several online sources on statistics available through the Members Toolbox. Click on "Members Login" on the HPS.org home page, sign in, and click on "HP Toolbox" and then "Statistics" under "Applied Topics."
Once you have determined the background characteristics, the mean and standard deviation for a given population, you can proceed to evaluate detection limits. Depending on the nature of the data being collected, the background data may be used to calculate the critical level, which defines the lower limit of radiation above background that is deemed statistically significant (see ATE answer to Question 6701 as an example of the calculation of critical level from count data). The lower limit of detection (and minimum detectable level) is a quantity larger than the critical level and obtainable from it. You or your employer may have other criteria that are to be used for defining a critical level and/or minimum detectable level, depending on your needs and intentions and the number of false conclusions you are willing to accept.
I wish you well in your survey work.
George Chabot, PhD, CHP


