Answer to Question #9707 Submitted to "Ask the Experts"
Category: Radiation Basics — Beta Particles (negative and positive) and Electrons
The following question was answered by an expert in the appropriate field:
I want to learn the difference between mean range and max range in betas. As I know, max range is used for shielding calculation. But then what is the mean range used for?
Your question is a good one since the notions of such quantities as charged particle range and depth of penetration in materials have significance in our interpretation and prediction of particle behavior. The concept of particle range in materials has different implications, depending on the nature of the charged particle, and different quantities related to the particle range are common.
For example, when electrons or beta particles of a given energy enter a material, they are prone to scattering in the material. The scattering results at times in changes in direction, with the possible result that the particle may travel a complex path in the material with some even scattering out of the material in the generally opposite direction from the direction of incidence. If one tries to measure the penetration of a beam of such particles through a given material by gradually increasing the thickness of the material and observing the number of electrons that penetrate through the material, the classic shape of the curve that results, when one plots the number penetrating, N, vs. depth or thickness, d, of the material, is similar to below:
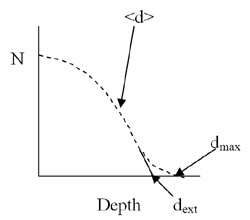
Beginning just beyond zero thickness, the number of electrons penetrating the thickness begins to decline even though the thickness is much less than the range of electrons. This is because of backscatter that occurs in the material, thus reducing the number of electrons penetrating the material. As the thickness increases, the number of electrons penetrating the thickness begins to decline more sharply. The point shown as
As a point of comparison with electrons/beta particles, we should note that when dealing with heavy charged particles, such as monoenergetic alpha particles for which appreciable scatter is not a significant factor, the above type of penetration curve has a different character. The upper part of the curve is more nearly horizontal until the depth approaches the range of the alpha particles; as the depth of penetration approaches the CSDA range, the curve descends much more sharply than for the case of electrons, and the tail of the curve is shorter. The result is that for such particles the values of dext and dmax are all within a few percent of each other.
The range that is often tabulated in reference compilations is a calculated quantity referred to as the CSDA (continuous slowing down approximation) range. This is calculated by integrating the inverse of the linear stopping power of the electron from zero energy up to the initial energy of the electron. It turns out that for lower-atomic-number materials the CSDA ranges of electrons are quite close to the dmax values—e.g., for carbon with an atomic number of six, electrons ranging in initial energy from 0.025 MeV to 10 MeV have dmax values that are about 95 percent of the CSDA ranges. For high-atomic-number materials the differences are greater; thus, for lead the dmax values are only about 60 percent of the CSDA ranges. Thus, for high-atomic-number materials, the CSDA range is not always a good estimator of the maximum depth of penetration.
The quantity dext in the above figure represents the so-called extrapolated penetration depth or extrapolated range. This quantity is useful when certain experimental measurements are made, most notably measurements made to determine the maximum energy of electrons or beta emitters. This extrapolated quantity is the value obtained by extrapolating the lower straight portion of the penetration curve to the point where it intersects the N = 0 axis. This provides a reasonable estimate of the range that can be evaluated in a comparison with a known beta emitter. The extrapolated range is more easily and more reliably determined than is the experimental dmax value because of the poor statistics associated with the number of electrons present near dmax, leading to a large uncertainty in the estimate of where the curve actually crosses the N = 0 axis.
We should note that the above discussion has treated the electrons or beta particles as being monoenergetic. If one is dealing with all of the beta radiation emitted by a particular beta emitter, the above considerations still apply to discrete energy particles, but the situation is complicated by the fact that the initial beta radiation includes beta particles whose energies range from zero to the maximum beta energy. Naturally, the maximum depth of penetration for a given beta emitter will depend on the maximum beta particle energy, and the above considerations still apply in a qualitative fashion.
In summary, when dealing with electrons or beta radiation, the specification of the range may or may not be a good estimate of the actual maximum depth of penetration. If the CSDA range is being used, and the material of interest has a high atomic number, the maximum penetration depth may be noticeably lower than the CSDA range. The mean ranges are not often directly useful for many practical situations, although they can be helpful in aspects of dosimetry in which one is concerned with the distribution of dose in tissue, since the mean range provides an estimate of the average depth within which one expects many of the beta particles to deposit most of their energy.
I realize the above is probably more of a discussion than you might have had in mind, but I think it is necessary to better understand some of the implications of your question. Hope it helps.
George Chabot, PhD, CHP


