Answer to Question #11989 Submitted to "Ask the Experts"
Category: Radiation Basics — Photons
The following question was answered by an expert in the appropriate field:
If I have a source of a given activity under water, how can I calculate the exposure dose above the water? I read that the gamma factor (which relates activity to exposure) is only for exposure in air; is there a gamma factor for water? If so, what's the right way to calculate it?
Here are additional details about my situation. The idea is to irradiate "smart materials" using a manganese-56 (56Mn) source in a reactor pool. My plan is to produce the 56Mn in the reactor and then move it under water to another place in the pool (far from the core). The initial activity planned will be approximately 5,600 gigabecquerels (GBq).
I have a few questions:
- If I want to irradiate my "smart materials" using the 56Mn source, how can I estimate the exposure rate under water—let's say 5 centimeters (cm) from the source?
- For safety reasons, what will be the exposure rate above the water? It will help me to determine how deep the source should be under water. The maximum exposure rate that the operator is allowed to receive is 1 millisievert per hour (mSv h-1) for five minutes.
- I didn't find a gamma factor for water, so I calculated it myself. The results surprised me: I found that it is just a bit higher than the gamma factor for 56Mn in air. This means that surprisingly, using the gamma factor for water produces a higher exposure rate. Why is the attenuation in water higher than in air?
I should first make a couple of pertinent observations. The first is that if you intend to irradiate materials that contain elements other than manganese, especially if such materials are metallic, you should take into account any radioactivity other than the 56Mn that may be produced and contribute to dose rate. Second, the gamma-ray constant for a given radionuclide may be for the quantity exposure, which implies that the dose receptor is a small volume of air irradiated under secondary charged particle equilibrium conditions; the imagined air volume may, however, reside in any medium of interest—air, water, lead, etc. In other cases, one may be using a gamma-ray constant that refers to equivalent dose in a small volume of tissue-equivalent material, or to some other biological dose quantity such as effective dose that is associated with a dose receptor that simulates the whole body, etc. Here again, the dose location of interest may reside in any material for purposes of dose calculations.
If you know the gamma-ray dose-rate constant in air, for which the expressed dose rate is that to air, it is a simple matter to convert the value to a dose-rate constant in water, for which the dose rate expressed is that to water. Here is a link to a convenient source of commonly used gamma ray dose constants; the values given in this compilation have dimensions of (millisieverts per hour)/(megabecquerels per meter2) (mSv h-1 m2 MBq-1).
The implicit assumption always made in calculating gamma-ray exposure-rate constants or dose-rate constants is that the condition of secondary charged particle equilibrium exists at the dose point location. If this is so, and the gamma-ray dose-rate constant for a radionuclide that emits a single photon energy in air is Γair, then the gamma-ray dose-rate in water is Γair(µen/ρ)water/(µen/ρ)air, where (µen/ρ)water and (µen/ρ)air are the mass energy absorption coefficients for water and air, respectively, at the photon energy of interest; ρ represents the material density. This ratio simply accounts for the relative effectiveness of one material compared to another in extracting energy from the photons of interest. Please note that if an exposure-rate gamma-ray constant is being used, you must first convert the calculated exposure rate to absorbed-dose rate in air before making the above type of transformation to dose rate in water. If multiple photon energies are involved, then you must perform an appropriately weighted summation to account for differences among the values of the mass energy absorption coefficients. For example, if photons of i different energies are emitted by a radionuclide, the water dose-rate constant would be related to the air dose-rate constant by:

where fi is the gamma yield of the ith energy photons (i.e., gamma rays of the ith energy emitted per disintegration of the radionuclide), and Ei is the energy of the ith photons. The ratio of the two summations represents the dose-weighted mean value of the water-to-air mass energy absorption coefficient ratio.
For 56Mn there are three major photons that account for most of the dose; their respective energies (and respective yields) are 0.847 megaelectronvolts (MeV) (0.989), 1.811 MeV (0.272), and 2.113 MeV (0.143). The values of the mass energy absorption coefficients can be found in various sources; here is a link to a National Institute of Science and Technology (NIST) page. Go to Table 4 for values for compounds/mixtures. Values of gamma-ray dose-rate constants for specific radionuclides may vary somewhat among tabulations prepared by different groups for several reasons, one of which relates to what dose quantity is being evaluated—e.g., exposure (which refers only to air as the irradiated target volume with the older special unit of roentgen often used), effective dose, equivalent dose to a small volume of tissue-equivalent material, etc. I mention this only for informational purposes and shall not discuss it further.
The calculations of gamma-ray dose-rate constants do not account for any photon attenuation between the source and dose point (except for attenuation that may prevail in the dose receptor, such as a whole-body phantom that might be used if effective dose constants are being evaluated). The reason your value for water was slightly higher than that for air was because the mass energy absorption coefficients for water at the energies of interest were slightly higher than those for air.
We should note that for the kind of problem you are dealing with, if the gamma dose-rate constant already uses biological equivalent dose or effective dose units (sieverts [Sv]), then it doesn't matter whether the dose point is in air or water. What does matter is that in employing the dose-rate constant you properly account for attenuation and buildup in the water between the source and the dose point. The typical general equation that describes the dose rate at a point in water or a point in air close to the water-air interface is of the form:

where E is the dose rate at the dose point; k is a collective constant to convert energy absorption rate per unit mass to dose rate in the desired units; A is the source activity; Ei is the energy of the ith photons; fi is as previously defined; B(µix) is the buildup factor for the photons of energy Ei in the attenuating medium (water in this case); µi is the linear attenuation coefficient for these photons in the attenuating medium (values may be found at the same NIST link cited above; they are the mass values and are readily converted to linear values by multiplying by the material mass density); x is the photon path length travelled in this medium as measured along a line connecting the source to the dose point; e-µix is the transmission factor of the ith photons through the attenuating material; µen,i/ρ is the mass energy absorption coefficient for the ith photons in the dose medium of interest (usually water or soft tissue if biological dose is being estimated); and d is the distance between the source and the dose point.
Virtually all commonly used buildup factors are calculated based on the assumption that the source is surrounded by an infinite volume of the attenuating material. When doses are calculated in air near the surface of a large volume of attenuating material, the estimated doses will tend to be somewhat conservative because of the lack of scattering material on at least one side of the dose point. You can find compilations of point isotropic source buildup factors in various references (e.g., Jaeger et al. 1968). You can find considerable additional information by searching the internet.
If the gamma-ray dose-rate constant is being used, as you have indicated, the dose-rate equation would be slightly different:
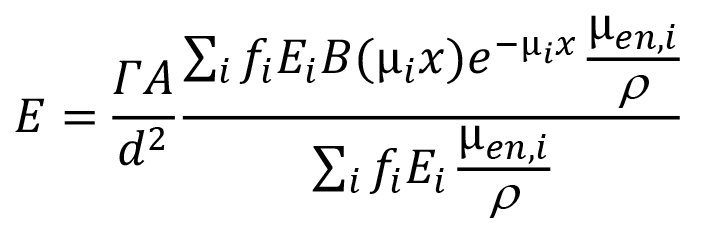
where A is the source activity (in the units that agree with those of the gamma dose-rate constant). Note that the second major term in this equation, the quotient of the two summation terms, represents the dose-weighted average value of the quantity B(µix)e-µix. If photons emitted by the source do not differ much in energy (which is not the case for the 56Mn photons), users will sometimes simplify the above somewhat by using a single value for µen/ρ, a single value for µi, and a single value for B(µx), based on the most dominant photon energy. In such a case the equation reduces to:
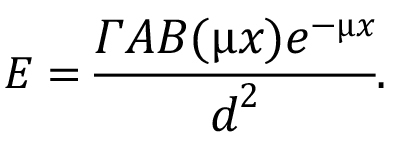
When dealing with point isotropic sources, as is implied if gamma-ray dose-rate constants are being used, values of buildup factors for specific values of µx for a given material can be looked up in tables in selected references. There are also various algebraic formulations that have been developed to represent the buildup factor, as are noted in Jaeger et al. (1968). You can find a discussion of the approach to some shielding calculations at this link.
George Chabot, PhD, CHP
Reference
Jaeger RG, Blizard EP, Chilton AB, Grotenhuis M, Honig A, Jaeger TA, Eisenlohr HH, eds. Engineering compendium on radiation shielding. Berlin, Germany: Springer-Verlag; 1968.


